Le pavillon
Loi d'expansion
Le pavillon est la partie de l'enceinte qui se charge d'amplifier le spectre qui sort de la chambre de compression. Le pavillon suit une loi d'expansion donnée. Plusieurs lois sont disponibles : hyperbolique, exponentielle (qui est un cas particulier de l'hyperbolique), Tractrix et Bessel. Ces lois ont pour but de fournir une surface en fonction d'une distance par rapport à la gorge du pavillon. Je me suis penché sur le cas hyperbolique plus en particulier, je laisse le soins à Dominique Pétoin de vous expliquer plus en détail les autres lois.
Pouquoi un pavillon hyperbolique ? C'est celui qui m'a semblé le plus adapté à mon projet, en effet alors que les autres lois ont un élargissement très rapide, la loi hyperbolique mise plus sur la longeur.
On en parle, on en parle mais on la voit toujours pas. Voilà la bête :
![]()
équivalente à :
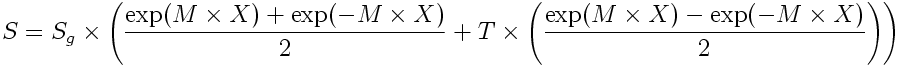
avec :
S = Surface en cm2 à la distance X.
Sg : Surface de gorge.
M : Coefficient d'expansion lié à la fréquence en m-1.
X : Distance entre la surface S et la surface Sg en m.
T : Coefficient qui modifie la forme et la vitesse d'expansion.
Coefficient M et T
Le coefficient M va agir sur l'expansion. Plus la valeur de M est importante, plus l'expansion est rapide. M est donné par l'équation suivante :
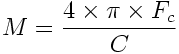
avec :
Fc : Fréquence de coupure théorique.
C : 343.4 m/s à 20°C; arrondi à 344.
Pour ce qui est de T, il agit sur la rapidité d'expansion près de la gueule. Un T faible se traduit par une expansion longue. T est choisi en fonction de la courbe de réponse du HP. Si elle est assez plane, on prend :
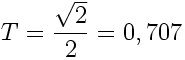
A noter que la loi d'expansion exponentielle est un cas particulier pour T = 1.
Tuning de coefficients
Il semble important de noter que dans le cas bien précis de T choisi à 0,707, il faut calculer M pour une valeur de Fc 1,5 fois plus petite pour obtenir des résultats optimums. Le calcul de M devient donc :
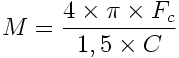
avec :
Fc : Fréquence de coupure théorique.
C : 343.4 m/s à 20°C; arrondi à 344.
Optimum
Enfin, pour reproduire la fréquence la plus basse désirée proprement, il faudra que la circonférence de la gueule corresponde à la longueur d'onde de la dite fréquence. Pour une onde acoustique, la longueur d'onde est donnée par la relation :
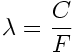
avec :
lambda : longeur d'onde en m.
C : 343.4 m/s à 20°C; arrondi à 344.
F : frequence considérée.
Conclusion : pour des basses fréquences la circonférence de la gueule augmente très vite. Exemple pour 20 Hz on obtient plus de 17 m. Heureusement, on peut limiter la casse dans la réalité. Le calcul précédent est valable dans le vide intersidéral (enfin non pas d'atmosphère pas de son); reformulons : espace infini. En effet sur notre bonne vieille Terre, on a tous, souvent, un sol au moins. Sol sur lequel vont se réfléchir les ondes, acoustiques notamment. Il en découle que si le pavillon ne se poursuit pas jusqu'à la circonférence optimum, le sol atténuera ce manque en doublant la longeur d'onde.
De la même manière, la longueur d'onde se voit multipliée par les coefficients suivants en fonction de la place de l'enceinte :
- 1 : enceinte en espace infini.
- 2 : écoute frontale, juste un sol.
- 4 : enceinte contre un mur.
- 8 : enceinte en encoignure.